El mundo de la geometría puede resultar fascinante y, a la vez, complicado. A menudo, nos enfrentamos a términos que pueden resultar confusos, como es el caso de las palabras cóncavo y convexo. Estas palabras se utilizan para describir las formas y curvaturas de diferentes objetos. Aunque pueden parecer similares a simple vista, en realidad poseen características distintas que es esencial conocer. En este artículo, te explicaremos en detalle las diferencias entre estas dos propiedades geométricas y cómo se aplican en la vida cotidiana.
¿Qué es una curva cóncava?
Una curva se considera cóncava si, en cualquier punto de la curva, la parte interior de la misma se encuentra en el mismo lado. Es decir, si trazamos una línea recta entre dos puntos de la curva, todos los puntos de esa línea se encuentran en el interior de la figura. Algunos ejemplos de objetos con curvaturas cóncavas incluyen:
- Una cuchara
- Una parabólica
- El interior de un cuenco
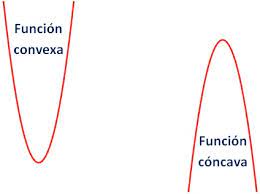
En matemáticas, una función se considera cóncava si su segunda derivada es negativa en un intervalo dado. Esto significa que la pendiente de la función decrece a medida que nos desplazamos de izquierda a derecha.
¿Qué es una curva convexa?
Por otro lado, una curva se denomina convexa cuando, al trazar una línea recta entre dos puntos de la curva, todos los puntos de la línea se encuentran en el exterior de la figura. En otras palabras, la parte interior de la curva se encuentra en lados opuestos. Algunos ejemplos de objetos con curvaturas convexas incluyen:
- Un balón de fútbol
- El exterior de un cuenco
- Un lente convexo
En el ámbito matemático, una función se considera convexa si su segunda derivada es positiva en un intervalo determinado. Esto implica que la pendiente de la función aumenta conforme nos desplazamos de izquierda a derecha.
Diferencias entre curvas cóncavas y convexas
Ahora que ya hemos definido ambos términos, es hora de destacar las principales diferencias entre cóncavo y convexo:
- Dirección de la curvatura: La dirección de la curvatura es la característica clave para distinguir entre ambos términos. En una curva cóncava, la curvatura se dirige hacia adentro, mientras que en una curva convexa, se dirige hacia afuera.
- Posición de la línea recta: Al trazar una línea recta entre dos puntos de una curva cóncava, todos los puntos de la línea se encontrarán en el interior de la figura. En cambio, en una curva convexa, todos los puntos de la línea se encontrarán en el exterior de la figura.
- Segunda derivada: En términos matemáticos, una función es cóncava si su segunda derivada es negativa en un intervalo dado. Por el contrario, una función es convexa si su segunda derivada es positiva en ese intervalo.
- Pendiente de la función: En una función cóncava, la pendiente decrece conforme nos desplazamos de izquierda a derecha. Por otro lado, en una función convexa, la pendiente aumenta en la misma dirección.
- Aplicaciones prácticas: Las curvaturas cóncavas y convexas tienen diferentes usos en la vida cotidiana. Por ejemplo, las lentes cóncavas son utilizadas en telescopios y cámaras, mientras que las lentes convexas se emplean en lupas y gafas.
Aplicaciones de las curvas cóncavas y convexas en la vida cotidiana
Las formas cóncavas y convexas están presentes en una gran cantidad de objetos y situaciones de nuestra vida diaria. A continuación, mencionamos algunas aplicaciones prácticas de estas curvaturas:
Cóncavas
- Lentes cóncavas: Estas lentes son más delgadas en el centro que en los bordes y se utilizan para corregir la miopía en gafas graduadas.
- Espejos cóncavos: Son espejos curvados hacia adentro y se emplean en telescopios y faros de automóviles, ya que concentran la luz en un punto focal.
- Parabólicas: Las antenas parabólicas tienen una forma cóncava y se utilizan para recibir señales de satélites, ya que concentran las ondas electromagnéticas en un punto.
- Diseño arquitectónico: En la arquitectura, las superficies cóncavas pueden emplearse en la construcción de techos o paredes para mejorar la acústica o estética de un espacio.
Convexas
- Lentes convexas: Estas lentes son más gruesas en el centro que en los bordes y se utilizan para corregir la hipermetropía y la presbicia en gafas graduadas.
- Espejos convexos: Son espejos curvados hacia afuera y se emplean en puntos ciegos de vehículos, cámaras de seguridad y cruces peatonales, ya que proporcionan un campo de visión más amplio.
- Diseño industrial: Las superficies convexas se utilizan en el diseño de productos como balones, cascos de motocicleta y carcasas de dispositivos electrónicos, entre otros, para mejorar su resistencia y ergonomía.
Conclusión
Las curvaturas cóncavas y convexas son propiedades geométricas fundament
ales que se encuentran en numerosos objetos y situaciones de nuestra vida diaria. Aunque pueden parecer similares, poseen diferencias clave en la dirección de la curvatura, la posición de la línea recta, la segunda derivada y la pendiente de la función.
Entender la diferencia entre cóncavo y convexo es esencial en campos como la óptica, la arquitectura, el diseño industrial y las matemáticas, ya que sus aplicaciones prácticas son diversas y tienen un gran impacto en nuestra vida cotidiana.
En resumen, una curva cóncava se caracteriza por tener una curvatura hacia adentro, con la línea recta trazada entre dos puntos de la curva situada en el interior de la figura. Por otro lado, una curva convexa presenta una curvatura hacia afuera, y la línea recta trazada entre dos puntos de la curva se ubica en el exterior de la figura. Conocer estas diferencias y aplicaciones nos permite comprender mejor el mundo que nos rodea y cómo las formas y curvaturas influyen en nuestras vidas.
Si deseas profundizar en el tema, te recomendamos visitar la siguiente fuente: Conceptos de geometría: cóncavo y convexo. Este enlace te permitirá ampliar tus conocimientos sobre las diferencias y aplicaciones de las curvas cóncavas y convexas en diversos campos y situaciones prácticas.
Linea concava
Una línea cóncava es aquella que presenta una curvatura hacia adentro, es decir, hacia la parte interna de la figura geométrica. Esta curvatura puede ser suave o pronunciada, pero en todos los casos, la línea se aleja de la dirección recta y forma un arco hacia el interior.
Las líneas cóncavas son comunes en figuras como círculos, elipses o parábolas, donde la curvatura hacia adentro es una característica distintiva. Estas líneas pueden ser utilizadas en diseño gráfico y arquitectónico para crear sensaciones de profundidad o movimiento, dependiendo de su aplicación y contexto.
En el ámbito matemático, las líneas cóncavas suelen ser objeto de estudio en geometría analítica, donde se analizan sus propiedades y ecuaciones para comprender su comportamiento y aplicaciones en diferentes áreas del conocimiento.
Una característica importante de las líneas cóncavas es que pueden ser parte de figuras complejas o simples, pero siempre mantienen su curvatura hacia el interior, lo que las diferencia de las líneas convexas que se curvan hacia fuera.