Las derivadas son fundamentales en el cálculo y en el análisis matemático. Son la base de muchas aplicaciones, así como importantes para la resolución de problemas matemáticos. Por lo tanto, es importante que los estudiantes comprendan la definición y los conceptos detrás de las derivadas. En este artículo, veremos qué son las derivadas, cómo se definen, y cómo se pueden resolver ejercicios con derivadas.
¿Qué son las derivadas y cómo se definen?
Definición de derivada
La derivada de una función es una medida de la tasa de cambio de una función matemática en un punto dado. En otras palabras, la derivada describe cómo cambia una función en un punto específico.
Fórmula y notación
La derivada de una función se representa por una letra «d» en minúscula y una «x» en minúscula, seguida por la función.
La notación para la derivada de una función «f» se escribe como:
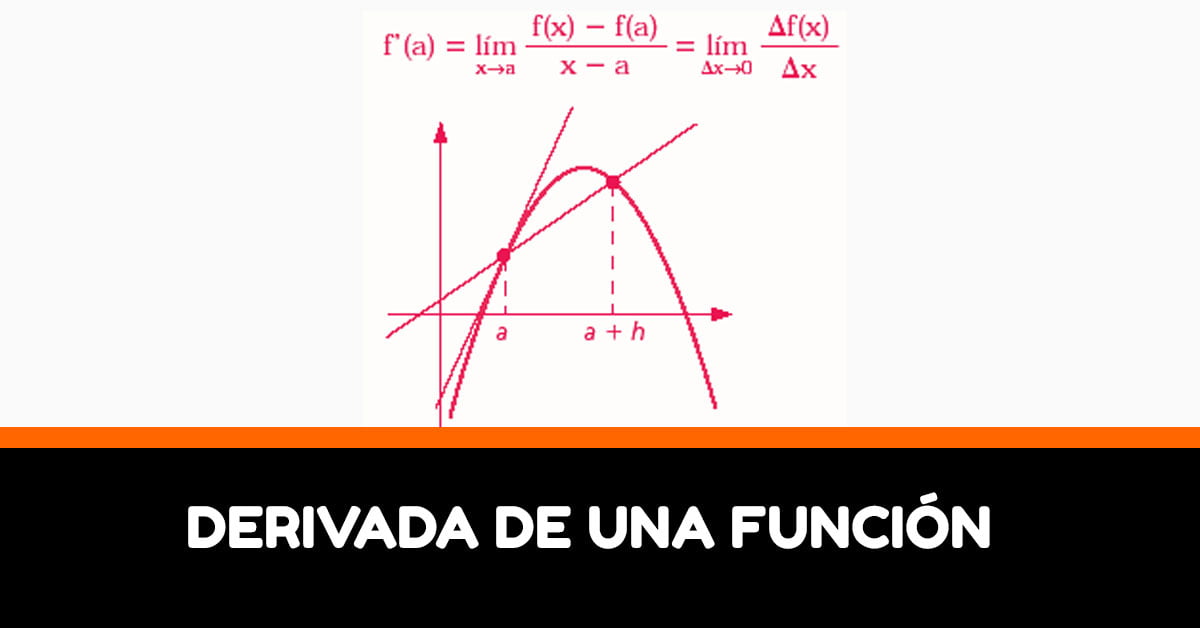
f'(x) = lim h->0 ( f(x+h) – f(x) )/h
Donde «h» representa el cambio en «x». En otras palabras, se calcula la tasa de cambio de la función en un punto determinado dividiendo el incremento en la función por el incremento en «x».
Interpretación geométrica de la derivada
La derivada también puede ser interpretada geométricamente. Si una función es diferenciable, entonces su gráfico tiene una recta tangente en cada punto. La pendiente de esa recta tangente es igual a la derivada de la función en ese punto.
Cómo calcular la derivada de una función en un punto
Concepto de derivada
El cálculo de la derivada de una función en un punto permite determinar la tasa de cambio de la función en ese punto. Para calcular la derivada de una función en un punto dado, se utiliza la fórmula establecida para la derivada de la función.
Reglas de derivación
Las reglas de derivación son herramientas valiosas para resolver ejercicios. Algunas de estas reglas incluyen:
1. La derivada de una constante es cero.
2. La derivada de una variable elevada a un exponente es igual a ese exponente multiplicado por la variable elevada a (exponente – 1).
3. La derivada de la suma o resta de dos o más funciones es la suma o resta de las derivadas de cada función.
4. La regla del producto establece que la derivada del producto de dos funciones es igual a la primera función multiplicada por la derivada de la segunda, más la segunda función multiplicada por la derivada de la primera.
5. La regla de la cadena establece que la derivada de una función compuesta es el producto de la derivada de la función exterior por la derivada de la función interior.
Derivadas laterales y derivadas de funciones trozo a trozo
También es posible calcular la derivada de una función en los límites derecho e izquierdo de un punto. Estas derivadas se llaman derivadas laterales.
Además, es importante destacar que algunas funciones están definidas trozo a trozo en un intervalo dado. Para calcular la derivada de una función como esta, es necesario encontrar la derivada de cada trozo individualmente y luego combinar esas derivadas en una función derivada.
Ejercicios resueltos de cálculo de derivadas
Derivadas de funciones exponenciales y logarítmicas
Para resolver ejercicios con derivadas de funciones exponenciales y logarítmicas, las reglas de derivación son fundamentales. Por ejemplo, si tenemos la función f(x) = e^x, la derivada es f'(x) = e^x. Si tenemos la función g(x) = ln(x), la derivada es g'(x) = 1/x.
Cálculo de la derivada de funciones trigonométricas
Las funciones trigonométricas también tienen reglas específicas de derivación. Por ejemplo, si tenemos la función f(x) = sin(x), la derivada es f'(x) = cos(x). Si tenemos la función g(x) = cos(x), la derivada es g'(x) = -sin(x).
Cálculo de la derivada de funciones con productos y cocientes
Las funciones que incluyen productos y cocientes también tienen reglas específicas para encontrar su derivada. Por ejemplo, si tenemos la función f(x) = x^2 / (x^2 + 1), la derivada es f'(x) = (2x(x^2+1) – x^2(2x)) / (x^2+1)^2.
Aplicaciones de las derivadas
Cálculo de pendientes y rectas tangentes
Las derivadas son fundamentales para el cálculo de pendientes y rectas tangentes. Si se tiene una función diferenciable, la pendiente de la recta tangente a la función es igual a la derivada de la función en ese punto.
Concepto de derivabilidad y continuidad
La función es derivable en un punto si la pendiente de la recta tangente a la función en ese punto está definida. La función es continua en un punto si la función y la tangente a la función en ese punto tienen el mismo valor.
Variación y comportamiento de la función en un punto
La variación instantánea de una función en un punto está dada por su derivada, lo que nos permite observar el comportamiento de la función en ese punto. Por ejemplo, si la derivada de la función es positiva en un punto, entonces la función tiende a aumentar en ese punto.
En conclusión, las derivadas son herramientas importantes para las matemáticas y su utilización es fundamental para el estudio de las funciones matemáticas y de sus aplicaciones en el mundo real. Con el conocimiento y la comprensión adecuadas de la derivación, los estudiantes pueden resolver problemas matemáticos y aplicar conceptos a situaciones del mundo real con mayor facilidad.