Las rectas paralelas son un concepto fundamental en matemáticas y geometría. Son relevantes en áreas como la arquitectura, diseño, ingeniería, física, entre otras. En este artículo, exploraremos la definición de rectas paralelas, cómo se pueden identificar y utilizar en diferentes ejercicios y aplicaciones.
¿Qué son las rectas paralelas?
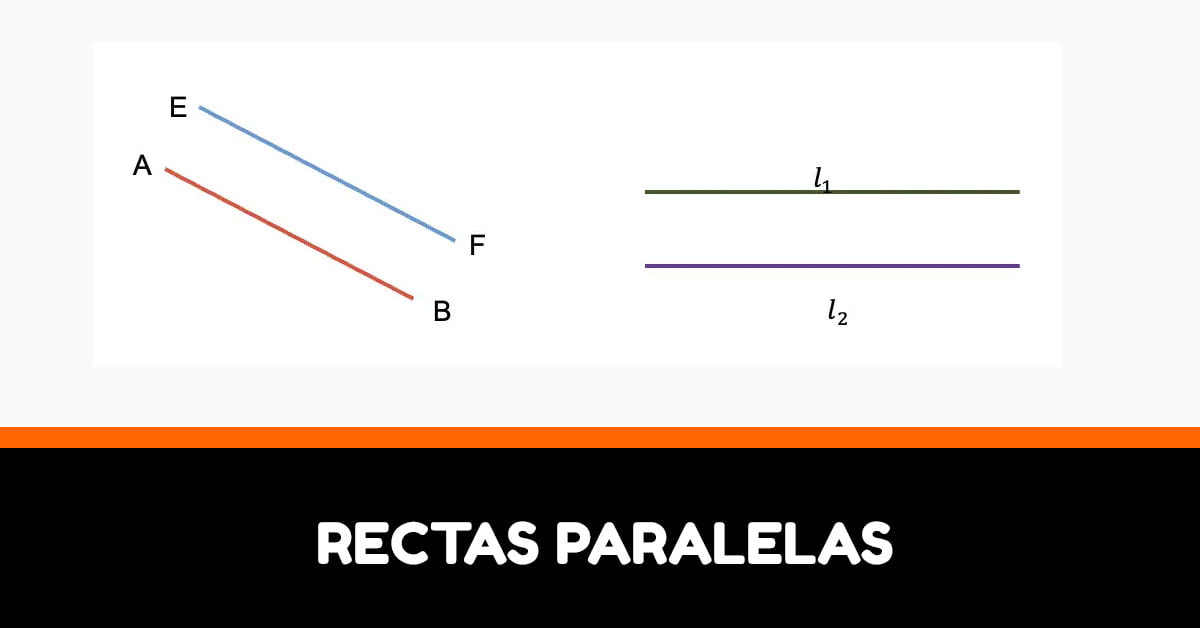
Las rectas paralelas son aquellas que se encuentran en el mismo plano y nunca se interceptan. Es decir, no tienen ningún punto en común.
Definición de rectas paralelas
Dos rectas son paralelas si mantienen la misma distancia entre ellas en todo su recorrido. Esto se debe a que su orientación es la misma y nunca se cruzan.
¿Cómo saber si dos rectas son paralelas?
Para determinar si dos rectas son paralelas, se debe comprobar si su pendiente es la misma. Si las dos rectas tienen la misma pendiente, entonces son paralelas.
Rectas paralelas en la vida cotidiana
Las rectas paralelas se pueden encontrar en múltiples situaciones cotidianas, como por ejemplo, en los postes de luz de una calle, los peldaños de una escalera, las rayas de un estacionamiento, los rieles del tren, entre otros.
Perpendicular y Secante
Además de las rectas paralelas, existen otros conceptos importantes en geometría relacionados con ellas.
Diferencia entre rectas paralelas y perpendiculares
Las rectas perpendiculares son aquellas que se cruzan en un ángulo de 90 grados. Es decir, se intersectan en un punto formando un ángulo recto.
Secante de dos rectas paralelas
La secante es una recta que cruza dos rectas paralelas en dos puntos diferentes.
Ángulos entre rectas paralelas y perpendiculares
Al igual que las rectas perpendiculares, las rectas paralelas también forman ángulos. Sin embargo, estos ángulos tienen una medida específica y constante. Entre ellas, se forman ángulos alternos internos, alternos externos, correspondientes y conjugados.
Ejercicios de Rectas Paralelas
Los ejercicios que involucran rectas paralelas son muy comunes en los estudios de matemáticas y geometría. A continuación, presentamos algunos ejemplos:
Ejercicio 1: Identificando rectas paralelas
Dados diferentes planos, encontrar dos rectas paralelas.
Ejercicio 2: Encontrando la ecuación de la recta
Dada una recta y su pendiente, encontrar su ecuación.
Ejercicio 3: Calculando la pendiente de una recta
Dados dos puntos en una recta, encontrar su pendiente y la ecuación de la recta.
Aplicaciones de las Rectas Paralelas
Las rectas paralelas tienen diversas aplicaciones que pueden ser útiles en diferentes áreas. A continuación, enumeramos algunas de ellas:
Distancia entre dos rectas paralelas
La distancia entre dos rectas paralelas se puede encontrar midiendo una distancia perpendicular a ambas líneas. Este concepto es utilizado en ingeniería y arquitectura, por ejemplo.
Funciones que involucran rectas paralelas
Las funciones lineales que involucran rectas paralelas son muy utilizadas en matemáticas y economía. Estas funciones ayudan a modelar relaciones entre diferentes variables.
Formación de figuras geométricas con rectas paralelas
Las rectas paralelas se utilizan en la creación de figuras geométricas como triángulos, rombos, trapecios, entre otros.
En conclusión, las rectas paralelas son un concepto clave en el mundo de las matemáticas y la geometría. Su comprensión y utilización permiten resolver diferentes problemas y aplicaciones en áreas como ingeniería, arquitectura, física, entre otras.
Lineas paralelas
Las líneas paralelas son dos o más rectas que nunca se cruzan, manteniendo siempre la misma distancia entre sí a lo largo de su recorrido. Este concepto es fundamental en geometría y permite establecer relaciones y propiedades interesantes entre diferentes figuras.
En geometría, las líneas paralelas se representan mediante una flecha doble que indica que las rectas no se cortan. Esta característica es importante para identificar patrones y simetrías en figuras geométricas, así como para resolver problemas matemáticos.
La propiedad más destacada de las líneas paralelas es que los ángulos correspondientes, alternos e interiores son iguales o suplementarios, lo que facilita el cálculo de medidas en figuras con líneas paralelas.
En la vida cotidiana, las líneas paralelas se encuentran en diversos objetos y estructuras, como edificios, carreteras, vías del tren y diseños arquitectónicos. Comprender este concepto es esencial para interpretar y analizar el entorno que nos rodea.
Que son rectas paralelas
Las rectas paralelas son aquellas líneas que nunca se cruzan entre sí, manteniendo siempre la misma distancia una de la otra.
En geometría, dos rectas se consideran paralelas si tienen la misma pendiente y nunca convergen, es decir, si se extienden indefinidamente en la misma dirección.
La propiedad fundamental de las rectas paralelas es que, a pesar de ser infinitas, nunca se encontrarán en ningún punto, manteniendo una separación constante a lo largo de su extensión.
En el plano cartesiano, las rectas paralelas pueden ser identificadas visualmente al observar que sus pendientes son iguales y que no se cruzan en ningún punto, formando ángulos correspondientes iguales entre las líneas y una tercera recta transversal.