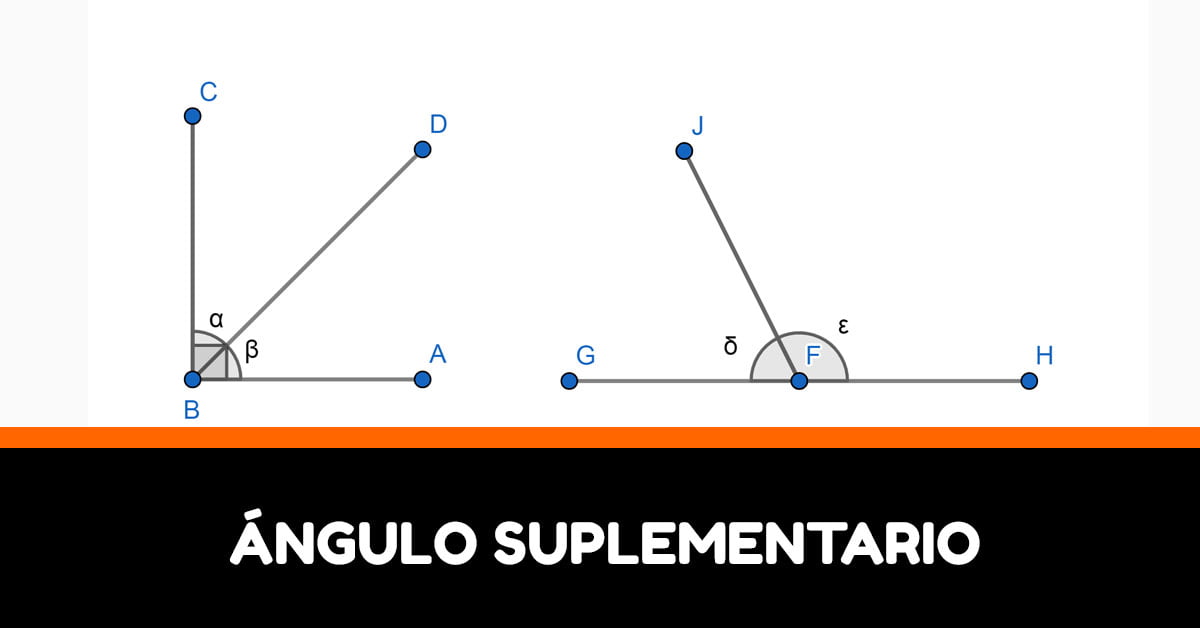
En este artículo, vamos a explorar el concepto de ángulo suplementario en matemáticas, incluyendo su definición y ejemplos prácticos. Además, analizaremos ejercicios resueltos y recursos adicionales para un mejor entendimiento del tema.
¿Qué es un ángulo suplementario?
Definición de ángulo suplementario
Un ángulo suplementario es aquel en el cual la suma de las medidas de dos ángulos es igual a 180°. En otras palabras, si dos ángulos son suplementarios, sus medidas suman un ángulo llano (180°).
Tipos de ángulos: suplementarios, complementarios y adyacentes
Existen diversos tipos de ángulos según sus características y propiedades. Un ángulo suplementario de un ángulo es aquel con el cual forma un ángulo llano, mientras que un ángulo complementario está relacionado con la suma de 90°, es decir, ángulos rectos. Por otro lado, los ángulos adyacentes son aquellos que comparten un vértice y un lado en común.
La suma de los ángulos suplementarios
Como mencionamos anteriormente, dos ángulos son suplementarios si la suma de sus medidas es igual a 180º. Esta propiedad es fundamental al trabajar con ángulos suplementarios y es una herramienta útil para resolver problemas en geometría y trigonometría.
¿Cómo identificar ángulos suplementarios?
Ángulos adyacentes y consecutivos
Los ángulos adyacentes son aquellos que comparten un vértice y un lado. En cambio, dos ángulos consecutivos son aquellos en los cuales el vértice del primer ángulo coincide con el vértice del segundo ángulo y un lado común está entre ambos ángulos. Ambos tipos de ángulos pueden ser suplementarios si cumplen con la condición de sumar 180°.
Medidas de ángulos: grados y radianes
Para identificar si dos ángulos son suplementarios, es necesario conocer sus medidas en grados o en radianes. Los ángulos se miden comúnmente en grados, y en el caso de ángulos suplementarios, la suma de sus medidas debe ser igual a 180°. También se pueden medir en radianes, en cuyo caso la suma de las medidas de dos ángulos suplementarios debe ser igual a π radianes.
Ángulos rectos y ángulos llanos
Un ángulo recto es aquel que mide exactamente 90°, y dos ángulos rectos forman un ángulo llano (180°). Por lo tanto, dos ángulos rectos siempre serán suplementarios. Un ángulo llano es aquel que mide 180°, y si dos ángulos suman un ángulo llano, son considerados suplementarios.
Propiedades y véase de los ángulos suplementarios
Propiedad de la suma de ángulos suplementarios
La propiedad fundamental de los ángulos suplementarios es que su suma es igual a 180°. Esto significa que si se conoce la medida de un ángulo, se puede determinar fácilmente el suplemento de dicho ángulo. Por ejemplo, si la medida del ángulo A es de 120°, su suplemento, el ángulo B, debe medir 60° (180° – 120° = 60°).
Ángulos suplementarios en la geometría
Los ángulos suplementarios aparecen con frecuencia en la geometría, especialmente al trabajar con polígonos, rectas paralelas cortadas por una secante y en la resolución de problemas de trigonometría. Entender cómo funcionan los ángulos suplementarios es crucial para resolver problemas en estas áreas de las matemáticas.
Ángulos suplementarios y trigonometría
En trigonometría, los ángulos suplementarios se utilizan para ayudar a resolver preguntas sobre triángulos y relaciones trigonométricas. Por ejemplo, si conocemos dos lados de un triángulo y un ángulo, podemos utilizar las propiedades de los ángulos suplementarios para encontrar los otros ángulos y completar el triángulo.
Ejemplos y ejercicios de ángulos suplementarios
Ejemplos prácticos de ángulos suplementarios
Uno de los ejemplos más comunes de ángulos suplementarios es el caso de dos ángulos rectos, donde cada ángulo mide 90° y su suma es 180°. Otro ejemplo podría ser un ángulo de 60° y otro de 120°, cuyas medidas suman 180°, convirtiéndolos en suplementarios.
Ejercicios resueltos de ángulos suplementarios
Hay una gran variedad de ejercicios que involucran ángulos suplementarios. Uno de ellos es hallar el ángulo suplementario de un ángulo dado, como el caso de un ángulo de 110° cuyo suplemento sería de 70° (180° – 110° = 70°). Otro tipo de ejercicio es determinar si dos ángulos son suplementarios al conocer sus medidas, como al verificar si un ángulo de 45° y otro de 135° lo son (45° +135° = 180°, por lo que sí lo son).
Métodos para resolver problemas de ángulos suplementarios
Resolver problemas de ángulos suplementarios generalmente implica tomar en cuenta la propiedad fundamental de su suma. También es útil emplear métodos algebraicos, como establecer ecuaciones basadas en las medidas de los ángulos y sus relaciones.
Recursos adicionales y tipo de información
Recursos en línea sobre ángulos suplementarios
Existen numerosos recursos en línea sobre ángulos suplementarios, incluyendo vídeos en YouTube, páginas web especializadas en matemáticas y aplicaciones educativas. Estos recursos pueden facilitar el aprendizaje y la comprensión del concepto de ángulos suplementarios.
Libros y materiales didácticos de matemáticas
Los libros de matemáticas y materiales didácticos, como cuadernos de ejercicios, también son excelentes recursos para profundizar en el tema de ángulos suplementarios. Estos materiales explican el concepto de manera detallada e incluyen ejemplos y ejercicios para poner en práctica lo aprendido.
Páginas web y aplicaciones para el aprendizaje de ángulos suplementarios
Además, existen páginas web y aplicaciones específcamente diseñadas para el aprendizaje de ángulos suplementarios y otros conceptos matemáticos. Estas herramientas pueden ser de gran ayuda para reforzar conceptos, practicar y mejorar el entendimiento sobre ángulos suplementarios.