Los ángulos son una parte fundamental de la geometría básica, por lo que conocer los diferentes tipos de ángulos y sus propiedades es esencial. En este artículo, nos enfocaremos en los ángulos adyacentes, desde su definición hasta cómo resolver ejercicios relacionados con ellos. Además, también se explicará la relación existente entre los ángulos adyacentes y otros tipos de ángulos como los opuestos por el vértice o los consecutivos.
¿Qué es un ángulo adyacente?
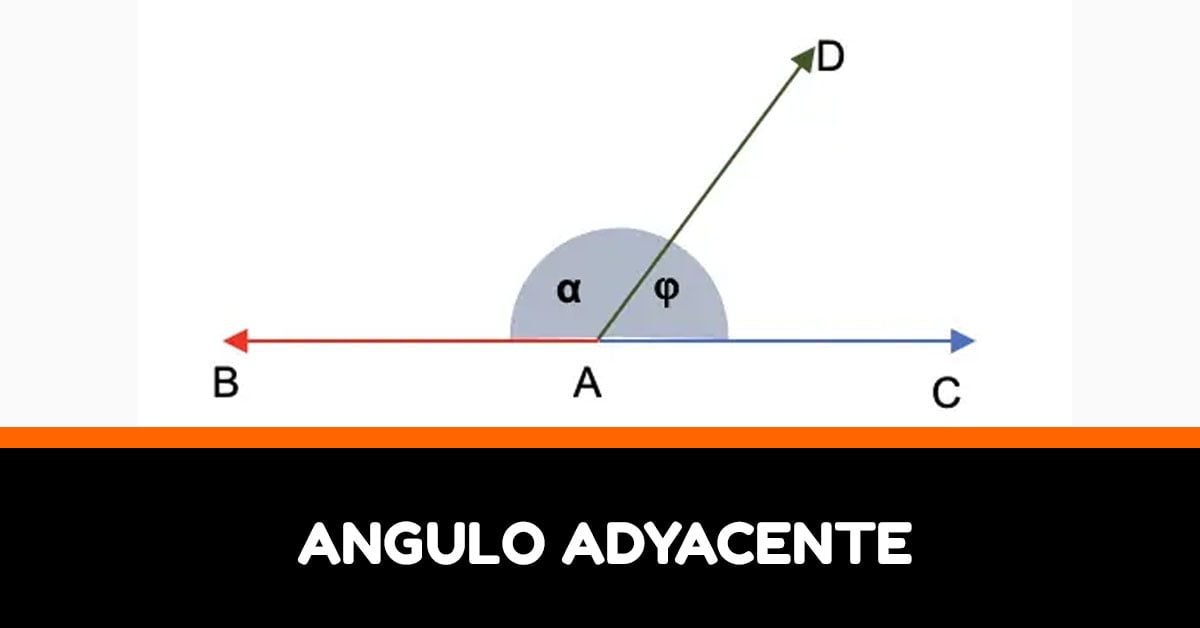
Para entender qué es un ángulo adyacente, es importante tener una definición clara de lo que es un ángulo en general. Un ángulo es la unión de dos semirrectas que tienen un punto en común, llamado vértice. Se denota con la letra alpha (α), beta (β), gamma (γ), entre otras. Por otro lado, un ángulo adyacente es aquel que comparte un lado y un vértice con otro ángulo. Es decir, ambos ángulos se encuentran uno al lado del otro.
En un ejemplo práctico, si tenemos dos ángulos, uno con medida de 60° y otro de medida de 120°, y ambos comparten un lado común, entonces estos son ángulos adyacentes.
Los ángulos adyacentes tienen una relación importante con otros tipos de ángulos. Por ejemplo, cuando dos ángulos adyacentes comparten el vértice y uno de los lados con otro par de ángulos adyacentes, éstos se llaman ángulos consecutivos y suman 180°. Si dos ángulos adyacentes opuestos por el vértice comparten el vértice y un lado común, entonces ambos ángulos tienen la misma medida.
Propiedades de los Ángulos Adyacentes
Para descubrir si dos ángulos son adyacentes, se debe verificar que tengan un vértice y un lado en común. Si ambos cumplen con esta condición, entonces efectivamente son ángulos adyacentes.
Otra propiedad de los ángulos adyacentes se presenta cuando comparten un lado y un vértice. En este caso, los dos ángulos forman un ángulo llano o un ángulo de 180°. Esto se puede demostrar utilizando la propiedad que establece que la suma de los ángulos internos de un triángulo es igual a 180°.
Por último, cuando dos ángulos adyacentes se encuentran en una recta, se dice que forman un ángulo recto o un ángulo de 90°. En este caso, ambos lados no comunes de los dos ángulos adyacentes son perpendiculares entre sí.
¿Cómo resolver ejercicios relacionados con ángulos adyacentes?
Para resolver ejercicios relacionados con ángulos adyacentes, se puede utilizar una combinación de teoría y fórmulas. A continuación, se presenta un ejercicio práctico:
Ejercicio de ángulos adyacentes
En la figura, ¿cuál es el valor de beta (β)?
Para resolver este ejercicio, debemos recordar que dos ángulos adyacentes siempre suman 180°. Además, ambos ángulos comparten un vértice y un lado. Utilizando la información proporcionada, podemos formar la siguiente ecuación:
α + β = 180°
Reemplazando los valores conocidos:
110° + β = 180°
Despejando β:
β = 70°
Por lo tanto, el valor de beta (β) es de 70°.
Es importante recordar que para poder descubrir la medida de un ángulo adyacente utilizando otros datos dados, se deben utilizar las propiedades mencionadas anteriormente como la suma de los ángulos internos de un triángulo o el hecho de que los ángulos adyacentes opuestos por el vértice tienen la misma medida.